Evolutionary Biology of Cancer in Turku, Finland--May 2013

I had the pleasure to travel to Finland this spring to work with my friends Kalle Parvinen and Anne Seppänen at the University of Turku (Turun Yliopisto). Kalle and I have known each other for nearly a decade and our research interests almost completely align—we both maintain strong interests in evolution of life history traits (especially dispersal) and the mathematics of adaptive dynamics, among other things. Anne is Kalle's PhD student, for whom I'm serving as a kind of secondary adviser, and she and I also share a number of research interests, particularly the evolution of malignant hallmarks in cancer. So far, we have produced two papers in dispersal evolution: one on the evolution of conditional (density-dependent) dispersal in metapopulations with small patch sizes (Parvinen et al. 2012) and another (Seppänen et al. 2012) on evolution of dispersal in the Bodie pika metapopulation (see here, for example). After this trip, there will be more on the way.

My travel to Finland and between Turku and Helsinki was supported by the Turku Centre for Computer Science (TUCS) and the Finnish Academy of Science and Letters, whom I thank for their gracious support.

While in Turku I gave a talk at the university that focused on recent results from my work on the evolution of angiogenesis in cancer. Angiogenesis—literally "vessel production" in Greek—is one of the "hallmarks of cancer" identified in two influential papers by Douglas Hanahan and Robert Weinberg (2000, 2011). In order for malignant tumors to grow and metastasize (spawn new tumors), they require blood vessels. To get them, tumors entice new capillaries to grow towards and into the tumor mass by secreting a variety of chemicals generally called tumor angiogenesis factors (TAF). The question we've been working on for some time now is, why do tumors secrete these chemicals?

You might think the answer is obvious—cancers secrete TAF because if they didn't they couldn't get new blood vessels and therefore couldn't grow. But that explanation cannot be right. Here's why. We know that tumor cells vary in ability to secrete TAF, and this variation is inherited. We also know that producing this signal is costly—it takes a nontrivial amount of ATP to produce and secrete TAF. So, tumor cells that naturally secrete less TAF would be expected to have more ATP for other things, including proliferation. Therefore, cells with lower angiogenesis potential apparently seem to "automatically" gain a proliferative, and therefore competitive, advantage against angiogenic cells. Since tumors are crucibles of competition, the advantage nonangiogenic clones enjoy will cause their population to grow faster than the population of angiogenic clones. In other words, the nonangiogenic clone becomes a tumor-on-a-tumor. Eventually, the nonangiogenic clone will dominate the tumor mass, but since it is not angiogenic, tumor vascular infrastructure will stagnate and eventually collapse. The nonangiogenic tumor ends up killing or damaging its host, but in this case the host is another tumor, not a human.

This phenomenon—a tumor-on-a-tumor—was first observed in a mathematical model I published in 2004. It came as a complete surprise. The model was designed to study tissue integration within cancers, but it coincidentally predicted the existence of these tumors-on-tumors. I suggested calling them "hypertumors" in parallel with the concept of "hyperparasite," which is a parasite exploiting another parasite.

It turns out that hypertumors are a special case of a phenomenon that is well known in evolutionary game theory. It's related somewhat to the economic game theory of John Nash, the main character in "A Beautiful Mind." Another manifestation is the "tragedy of the commons," the idea that resources that benefit all (public goods) tend to get exploited and eventually destroyed by cheating "free-riders" who refuse to invest in the public good but still enjoy its benefits.

For example, consider a farming community in which everyone tends the crops on which all depend for survival. Along comes a family of strangers who settle in the community. They become friendly with the neighbors and pretend to work in the fields, but really just take it easy and don't work hard. Nevertheless, they still get the same amount of produce as everyone else, so become more fat than the others. Along comes a deadly famine. The hardest working families suffer the most death because they habitually expend the most energy but get no more food. The family of free riders suffers the least. If work ethic were inherited, then in the next generation there would be fewer hard workers and more free riders. After many generations and a series of famines, eventually the community would be mostly free riders, the fields would be less productive because they are receiving less care, and the whole community suffers. Because work ethic is genetic, the free riders are unable to reverse course because they are habitually lazy; they won't tend the fields but retain their advantage over those who do. Ultimately, if conditions don't change, the community dies out. This evolutionary phenomenon has been observed in nature, in different contexts than farming communities, and is precisely analogous to the hypertumors predicted in 2004.

Real hypertumors, on the other hand, have not been observed—yet. There are a number of potential reasons why not, but the most glaring is that they are apparently not that common if they occur at all. To explore why they are not common, I needed a better model. (Remember, the 2004 version wasn't built to study hypertumors.) So, recently my colleague, Dieter Armbruster, and students Joe Juliano and Scott Bickel, and I have studied two related models of the phenomenon, which were the focus of my talk in Turku. The first, which Dieter and I published in the journal, Mathematical Biosciences and Engineering last year (2012), adds a cost to angiogenesis that the 2004 model lacked. The cost comes through the energy required to produce the signal. Adding this cost required us to model not just tumor dynamics but also adenylate (ATP, ADP and AMP) dynamics inside cells. It turns out that the adenylate model, which was an extension of a well-studied model by a Russian group (Martinov, Ataullakhanov, Vitvitski and their colleagues), had a very interesting property that may explain how angiogenesis evolves even though, as we saw above, natural selection tends to disfavor it. Our model and that of the Russians both predict that resting cells, as they begin to ramp up metabolic rate by burning more ATP per unit time, end up increasing their total stores of ATP (at equilibrium). In other words, they burn ATP at a higher rate but end up with more in the end. It would be as if you go shopping, and the more you buy the more your bank account grows. That seems completely backwards, but that's what the models predict. That's also what the Russian group observed in real cells. Now, the key phrase is this—"resting cells." Metabolically active cells behave as you would expect; the model predicts that the more they burn ATP, the less ATP they end up with.

That phenomenon is not only intriguing, but it also potentially explains how angiogenesis arises in actual tumors and why hypertumors are rare. Without going into a lot of detail about the technique (those interested in such details, stay tuned for an upcoming post), Dieter and I showed that there exists in this model an angiogenic phenotype that is what the famous biologist John Maynard Smith called an "evolutionary stable strategy," or ESS. This is a phenotype that, when overwhelmingly common in a population, cannot be outcompeted by any other possible phenotype that might arise as a rare mutant. But, this ESS is an odd one—it's an evolutionary repeller, meaning that over time natural selection will push the population away from the ESS phenotype (the slide below illustrates this result). [A note to dynamicists: Maynard Smith's concept of evolutionary stability in this context is not our concept of stability. An ESS may not be asymptotically stable, or even stable, in our sense. To us, an ESS is really just an evolutionary fixed point.]

This slide shows two things. First, by pushing the population away from the ESS, selection drives angiogenesis to extremes, either low (vascular hypoplasia) or high (vascular hyperplasia). Either case would yield an eventual hypertumor. Both vascular hypo- and hyperplasia have been observed in real tumors, although the mechanism hypothesized here has never been demonstrated. Second, the selection gradient is very, very shallow because angiogenic signaling is not energetically costly compared to proliferation. So selection confers, at best, only a slight advantage. Therefore, this result predicts that angiogenesis is always on an evolutionary transient (it never settles to an evolutionary equilibrium because the "equilibrium" values exist only in conditions that cause tumor necrosis, which might be expected to happen slowly).

Among the weaknesses of this result is that it tells us neither the probability a hypertumor arises before a tumor becomes deadly, nor what the dynamics of angiogenic potential, and therefore tumor vasculature, is likely to be. (The reason is technical and has to do with a limitation in the adaptive dynamic technique used; again, those interested in technicalities, keep your eyes open for a post on its way soon.) However, we can get at these questions with a simulation, which Scott Bickel and Joe Juliano put together. Their simulation completely confirmed the mathematical result of the MBE paper (see slide below).

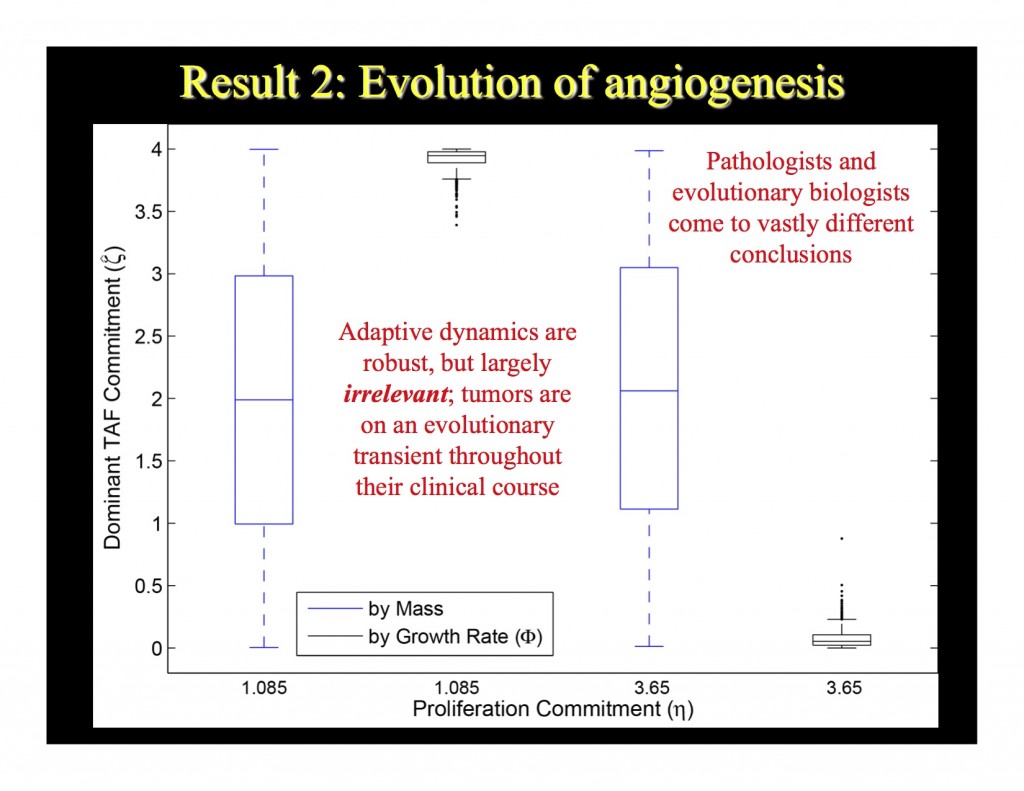
But the simulation also suggests that the probability of a clinically relevant hypertumor (one that arises before the tumor reaches lethal size) depends on how another trait—namely, proliferative potential—evolves. So our next step is to model angiogenic and proliferative potential as they evolve together.

Stay tuned.

Slides of this talk are available here: Evolution of proliferation and the angiogenic switch in phenotypically diverse tumors

References

Bickel, S. T., J.D. Juliano and J.D. Nagy. 2013. Evolution of proliferation and the angiogenic switch in tumors with high clonal diversity. Submitted to: PLoS ONE.

Hanahan, D. and R.A. Weinberg. 2000. The hallmarks of cancer. Cell 100:57-70.

Hanahan, D. and R.A. Weinberg. 2011. Hallmarks of cancer: The next generation. Cell 144:646-674.

Nagy, J.D. and D. Armbruster. 2012. Evolution of uncontrolled proliferation and the angiogenic switch in cancer.  Mathematical Biosciences and Engineering 9:843-876.

Nagy, J.D. 2004. Competition and natural selection in a mathematical model of cancer. Bull. Math. Biol. 66: 663-687.

Parvinen, K., A. Seppänen and J.D. Nagy. 2012. Evolution of complex density-dependent dispersal strategies. Bulletin of Mathematical Biology 74:2622-2649. DOI 10.1007/s11538-012-9770-9.

Seppänen, A., K. Parvinen and J.D. Nagy. 2012. Evolution of dispersal in American pika (Ochotona princeps) metapopulations. Evolutionary Ecology Research 14:1-29.