Biological Stoichiometry of Cancer

For the past decade, Jim Elser, Yang Kuang and I, among others, have been working on applying a unifying theory in ecology called ecological stoichiometry to oncology. The general theory (not the application to tumors) is elaborated in a book by Jim and Bob Sterner (Sterner and Elser 2002). In fact, this application really represents a special case of the generalization of ecological stoichiometry to all of biology, a principle called biological stoichiometry (Elser et al. 2000; see also Jim's pubs page). The basic idea is, as Jim puts it, that "life is made of stuff," with the consequences summarized on the following slide from a talk I gave in Helsinki in spring 2013:

The key biochemical constraint for rapidly dividing cells, one might think, is the need for ribosomes to build the proteins required for proliferation. Ribosomes are very P-rich structures, so actively proliferating cells should have a relatively low C:P ratio (lots more P compared to biomass, measured by C, than normal cells). In fact, this is precisely what is seen across a wide variety of taxa (see e.g., Elser et al. 2003a).

Since tumors are often claimed to be characterized as "uncontrolled growth," one therefore expects them to be P-rich. We made this argument, with some supporting modeling, a decade ago (Elser et al. 2003b, Kuang et al. 2004), encouraged mainly by micrographic studies suggesting that cancer cells contain many more ribosomes than healthy cells in the same tissue. However, when we tested this hypothesis in four different tumor types--lung, colorectal, liver and kidney carcinomas--we found support for the idea only in the first two, as shown on the following slide (figure from Elser et al. 2007):

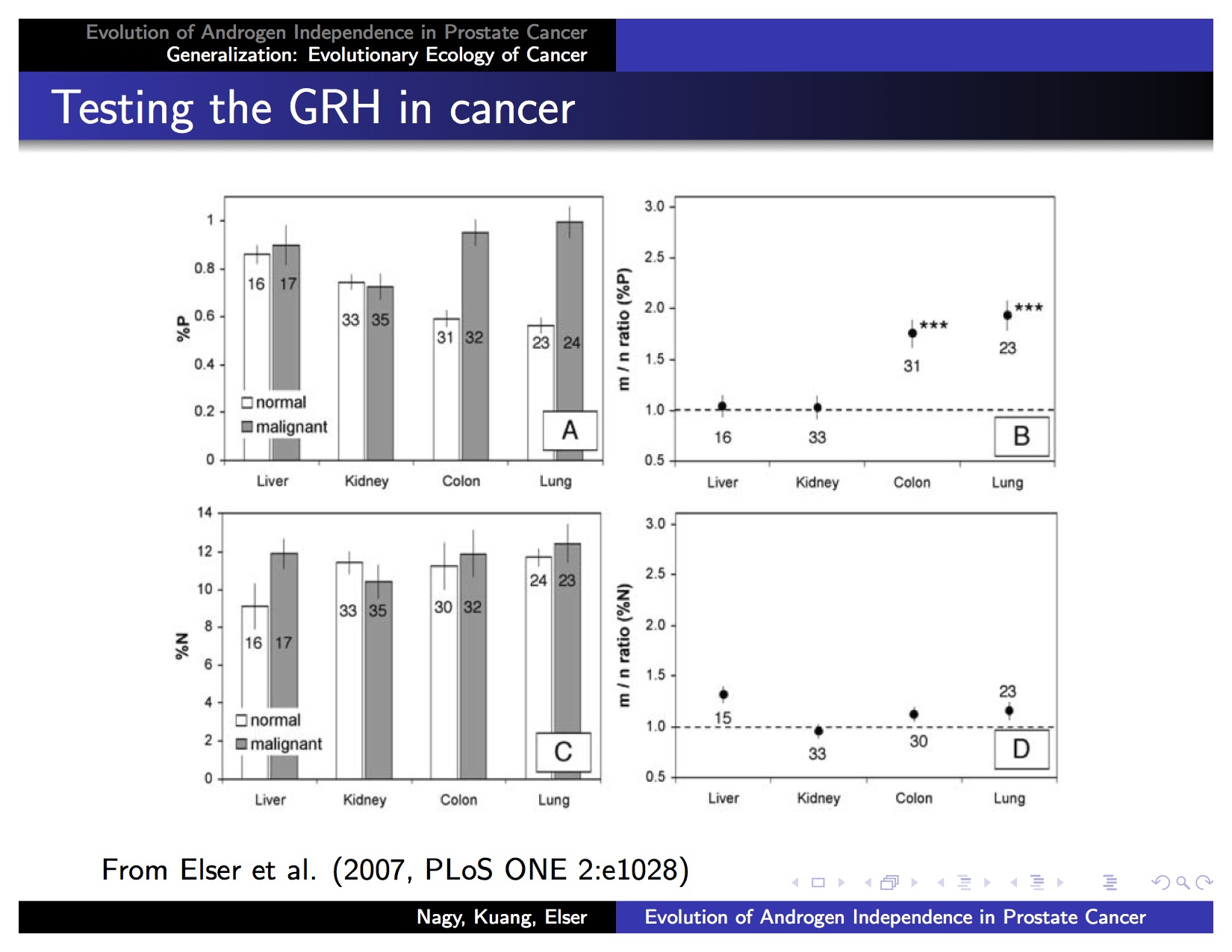
Panel B is the key. It shows the dry mass %P ratio of malignant to matched healthy tissue from the organ of origin in the same patient. A ratio of 1 means that the %P by mass is the same in both tumor and healthy tissue. (Bars represent 95% confidence intervals.) Notice that liver and kidney ratios are both near unity, but colon and lung ratios are both approaching 2, meaning that in these last 2 tumor types, malignant cells have about twice the amount of P by mass than does healthy tissue from the same organ in the same person. So, our prediction worked for colon and lung cancer, but not for liver and kidney. Naturally we immediately asked, what's going on?

Grappling with that question eventually led us back to a famous, often inappropriately maligned, idea of Robert MacArthur and E. O. Wilson. In chapter 7 of their classic 1967 book, The Theory of Island Biogeography, MacArthur and Wilson address how selection acts differently on islands compared to mainlands. Imagine a newly created island recently colonized by a species from the mainland. Since the colony is likely to be small relative to the island's resources, there will be little density-dependent feedback on mortality and (or) births. This lack of a nonlinear check on growth will tend to favor phenotypes with the highest intrinsic rates of increase, all else being equal. Here, intrinsic rate of increase is the difference between birth rate and death rate in the most favorable environment for a species. General models of population growth are often written as something of the form,

dx/dt = r(x,t) x(t),

where x(t) the population size at time t. The function r is the per capita growth rate, which may depend on the population size or time or both. However, if there were no density-dependent feedback and a constant environment, then r would also be constant. In that case the model reduces to the linear ordinary differential equation (ODE),

dx/dt = rx(t),

which has exponential solution x(t) = x0 exp(rt), where x0 is the initial population size (at time = 0). So, in such an environment (constant with no nonlinear feedback), MacArthur and Wilson, like Lotka, Wright, Fisher and Haldane before them, recognized that selection will tend to maximize, within its physiological constraints, the value of the constant parameter r. MacArthur and Wilson referred to this as r-selection.

Now, consider what tends to happen as the colony ages. If the environment stays constant and permissive, then the colony will tend to expand into all available space on the island, eventually running into some resource limitation. Eventually, the limiting resource will become increasingly scarce for each individual. This is precisely a nonlinear negative feedback on population size. Under the right conditions, when this feedback becomes intense enough, the population will use the resource at precisely the same rate at which the resource is naturally replenished. If, in that case, the population growth rate is zero--number of births precisely replaces number of deaths every year (on average)--then we say the population has reached "carrying capacity." In the Verhulst (or logistic) differential equation of population growth, viz.

dx/dt = rx(t)(1-x(t)/K),

the intrinsic rate of increase is often denoted r, and the carrying capacity is K, as I've done here. (Note that MacArthur and Wilson did not refer to the Verhulst equation in their explanation; they argued from phase plane analysis of a much more general model.)

MacArthur and Wilson suggest that if the island population approaches carrying capacity, natural selection would switch from r-selection into a different selective mode they called K-selection. In their own words,

As an example of how K selection and r selection can be in opposition, consider different situations in which crowding can either reduce the per capita food supply to a precariously low level, or else not have this effect. In an environment with no crowding (r selection), genotypes which harvest the most food (even if wastefully) will rear the largest families and be most fit. Evolution here favors productivity. At the other extreme, in a crowded area, (K selection), [sic] genotypes which can at least replace themselves with a small family at the lowest food level will win, the food density being lowered so that large families cannot be fed. Evolution here favors efficiency of conversion of food into offspring. [pg. 149.]

As originally formulated, the r- and K-selection idea suffers the characteristic ambiguities and imprecisions of the heuristic and analogical style of theory common in mid-20th century biology. It couldn't be defended on solid mathematical and empirical grounds. So now it has become fashionable in some circles to dismiss any reference to it a priori. However, if used carefully the notion still bears fruit. Its stylized and simplified picture of selection favoring reproductive potential above all else in disturbed environments but tending to favor lower reproductive output with greater investment in survival in more stable environments remains relevant to this day.

And that relevancy extends to cancer biology, or so we hypothesize. How do tissues in which lung and colon carcinomas arise differ from those in the kidney and liver? An answer immediately surfaces--lung and colon epithelium, the sources of the cancers we studied--are much more exposed to insults from the external world than are tissues in kidney and liver because they are in direct contact with the external world. Cell turnover rates in the former two organs are therefore much greater than in the latter. Or, put into the language of ecology, lung and colon epithelial ecosystems are more highly disturbed than are those in kidney and liver. If cancer arises in any of these tissues, the tumor lineages (clones) apparently suspend cooperation with surrounding cells and begin to compete with them for resources. In the highly disturbed environments of the lung and colon, resources (phosphate, glucose, glutamine, etc.) are relatively common. Therefore, we hypothesize that in such environments, selection will favor mutations that maximize proliferation rate, and we recognize this as analogous to MacArthur and Wilson's notion of r-selection, understood generally, and so we honor them by calling it that. In contrast, the liver and kidney environments are much more stable. Therefore, tumor cells experience more nonlinear feedback on population size due to competition. We hypothesize that in such cases selection favors resistance to apoptosis and other sources of mortality. Again, we see the parallels here with MacArthur and Wilson's K-selection, so we apply that term here (see figure below).

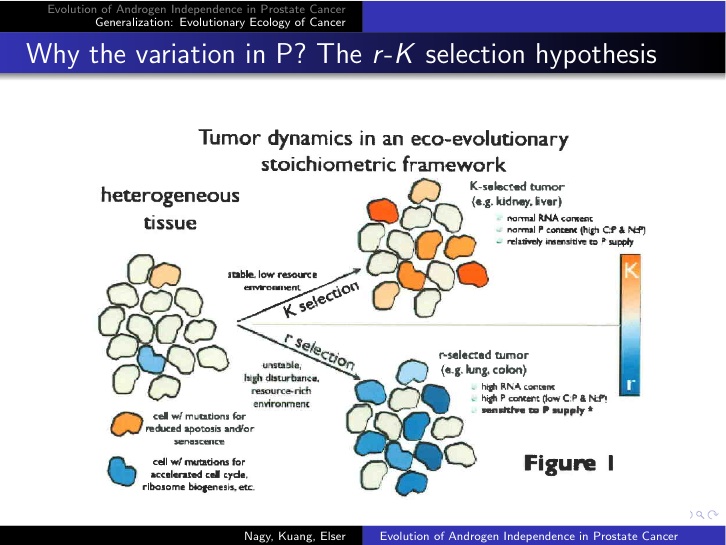
So, what empirical evidence is there for or against the "r-K-selection" hypothesis in cancer? There should be a lot--either way--because it makes very simple, testable predictions. Most notably, the hypothesis predicts that tumors in high disturbance tissues like lung and colon epithelium should be susceptible to P limitation. That suggests a simple experiment. Find tumors that have evolved rapid proliferation rates. Implant them in athymic mice (mice with no thymus gland and therefore profoundly immunologically impaired). Feed some of the mice a rich-P diet and others a low-P diet. If the hypothesis is correct, tumors in mice fed the rich-P diet will grow faster than tumors in the other mice. The same experiment performed on mortality-resistant, less proliferative tumors will show no difference between treatments.

Although no one has done precisely this experiment, the hypothesis is supported by two intriguing studies. The first, by Jin et al. (2009), showed that lung cancers in mice grow significantly faster when the mice are fed a high-P diet compared to a normal-P diet, as predicted by our hypothesis. In the second study, Camelier et al. (2010) saw something similar in a mouse model of skin cancer. A strain of mouse in which highly reproducible skin cancers can be induced were fed normal- and low-P diets. Mice on normal diets developed significantly more skin tumors (papillomas), leading the authors to conclude "that elevated phosphate promotes cell transformation and skin tumorigenesis." The mechanism was linked to a protein called N-ras, a G-protein involved in cell signaling. It's a key upstream element in a transduction cascade that ultimately upregulates a host of pro-proliferation genes, among them genes for ribosome synthesis (Hannan et al. 2011). Again, this fits our prediction. Skin is a highly disturbed environment, so we expect these tumors to be "r-selected." They should therefore be susceptible to P limitation. And they are. That susceptibility is predicted to arise because selection favoring high proliferation rates must, as a necessary corollary due to physiological constraints on how cells work, also generate demand for large amounts of P to build the ribosomes to support proliferation. And, dietary P affects activity of a protein that controls, in part, ribosome biogenesis.

Tantalizing as these results are, they are not definitive, largely because the studies were not designed to test our hypothesis. Direct tests of the notion have not been completed, but not due to any laziness on our part. We have the studies designed and ready to go but for one thing--funding. Experiments cost money, and we--Jim Elser, collaborators from the Translational Genomics Research Institute (TGen) Mike Berens and Mike Barrett and I--have struck out trying to get interest from NSF, NIH and even private funding. There is more modeling to be done, but that can only take us so far. Ultimately, the predictions our hypothesis and models make can only be tested at the bench. So, for now, the idea languishes.

References

Camalier, C.C., M. R. Young, G. Bobe, C. M. Perella, N. H. Colburn and G. R. Beck. 2010. Elevated phosphate activates N-ras and promotes cell transformation and skin tumorigenesis. Cancer Prev. Res. 3:359-370.

Elser, J. J., K. Acharya, M. Kyle, J. Cotner, W. Makino, Theresa A. Markow, T. Watts, S. Hobbie, William F. Fagan, J. Shade, J. Hood and Robert W. Sterner. 2003a. Growth rate-stoichiometry couplings in diverse biota. Ecol. Lett. 6:936-943.

Elser, J. J., J. D. Nagy and Y. Kuang. 2003b. Biological stoichiometry: An ecological perspective on tumor dynamics. BioScience. 53:1112-1120.

Jin, H., C.-X. Xu, H.-T. Lim and et al.. 2009. High dietary inorganic phosphate increases lung tumorigenesis and alters Akt signaling. Am. J. Respir. Crit. Care Med. 179:59-68.

Kuang, Y., J. D. Nagy and J J. Elser. 2004. Biological stoichiometry of tumor dynamics: Mathematical models and analysis. Disc. Cont. Dyn. Syst. B 4:221-240.

Hannan, K. M., E. Sanij, N. Hein, R. D. Hannan and R. B. Pearson. 2011. Signaling to the ribosome in cancer--It is more than just mTORC1. IUBMB Life 63:79-85.

MacArthur, R. H. and E. O. Wilson. 1967. The Theory of Island Biogeography. Princeton U. Press, Princeton, N. J.

Sterner, R. W. and J. J. Elser. 2002. Ecological stoichiometry : the biology of elements from molecules to the biosphere. Princeton U. Press, Princeton, N. J.